Conditional GANs (cGANs) and its variations

Back to basics. As a series of my “reinventing-the-wheels” project to understand things well, I took some time to reimplement Conditional Generative Adversarial Nets from scratch. This is a note on it.

Background

Generative Adversarial Networks was introduced by Ian Goodfellow in 2014. Since then, so many different types of GANs have been invented and GANs have been one of the hottest topics in the machine learning community.

A few months after the original GAN paper submitted, Conditional Generative Adversarial Nets (cGAN) was proposed (according to arXiv, the original GANs paper was submitted on 10 Jun 2014 and cGANs paper was submitted on 6 Nov 2014).

The core motivation of the cGANs paper was that although GANs showed successful image generation ability, there was no way to control or specify a certain type of image to generate. (for instance, specify ‘1’ in MNIST dataset)

The proposed conditioning method is to simply provide some extra information y, such as class labels, to the generator and the discriminator.

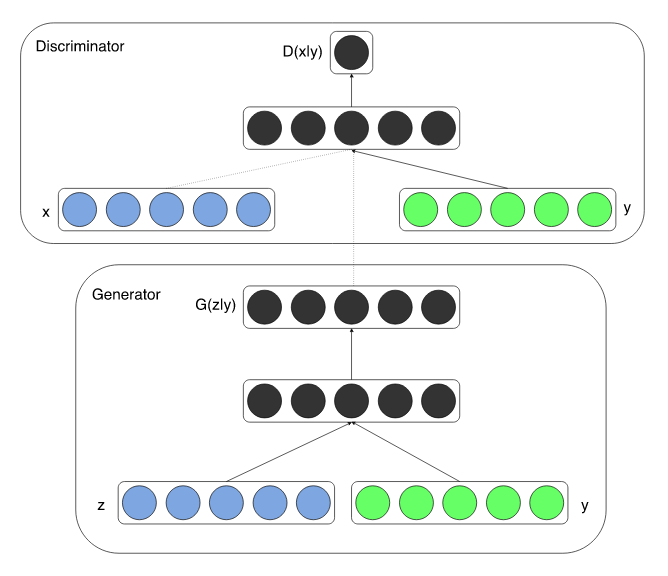
Figure from Conditional Generative Adversarial Nets paper

The authors presented its effectiveness by showing MNIST experiments in which the generator and the discriminator were conditioned on one-hot class labels.

Implementation

OK, time to code. My implementation of the original GANs (gan.py is the main and models are defined in models/original_gan.py) and Conditional GAN.

The main differences are the following parts:

1. Model definition: now the input size of the first layer of the network is z_dim+num_classes.
2. Training: Concatenating noise z and label which is an one-hot vector.

Model definition

class Generator(nn.Module):                                              
    def __init__(self, batch, z_dim, out_shape, num_classes):                             
        super(Generator, self).__init__()                                 
                                                                         
        self.batch_size = batch                                          
        self.z_dim = z_dim                                                    
        self.out_shape = out_shape                           
        self.num_classes = num_classes                                                    
                                                                                                                                        
        self.fc1 = nn.Linear(z_dim+num_classes, 256) # simple concat
        ...

Similarly, the discriminator is modified to take the input images concatenated with an one-hot label.

Training

generated_imgs = generator( torch.cat((z, label), dim=1) )

Quick tip: I found torch.Tensor.scatter_ useful to convert class labels of 1 dimension into N-dim one-hot encoding. (e.g. convert [3] into [0,0,0,1,0,0,0,0,0,0] where N=10). Since the labels of MNIST data are a list of integers, I convert this into an one-hot vector of [batchsize x num of classes] by implementing the following function.

def convert_onehot(label, num_classes):
    """Return one-hot encoding of given list of label
    Args: 
        label: A list of true label
        num_classes: The number of total classes for y
    Return:
        one_hot: Encoded vector of shape [length of data, num of classes]
    """
    one_hot = torch.zeros(label.shape[0], num_classes).scatter_(1, label, 1)
    return one_hot

Experimental results

The left image is the data in a particular batch and the right image is the generated image conditioned by the label which corresponds to the numbers in left figure.

As you can see, the generated digits in the right image is the same with the left one. This is because the model is conditioned by the label and can be used to generate that number. Wow, good job, it’s so simple but actually working!

Further reading

I read cGANs with Projection Discriminator and found it’s interesting. They proposed a novel way to incorporate the conditional information into the discriminator of GANs.

In this paper the authors introduced their “projection based way” which is different from simply concatenating additional information to the input vector. According to the author, their method ‘respects’ the role of the conditional information. Here is the quote from the paper.

We propose a novel, projection based way to incorporate the conditional information into the discriminator of GANs that respects the role of the conditional information in the underlining probabilistic model. This approach is in contrast with most frameworks of conditional GANs used in application today, which use the conditional information by concatenating the (embedded) conditional vector to the feature vectors.

These are the variations of cGANs proposed so far. (a) is the one I just implemented and the (d) is the projection based method. (By the way this figure is really nice to quickly understand the variations of the way to conditioning GANs)

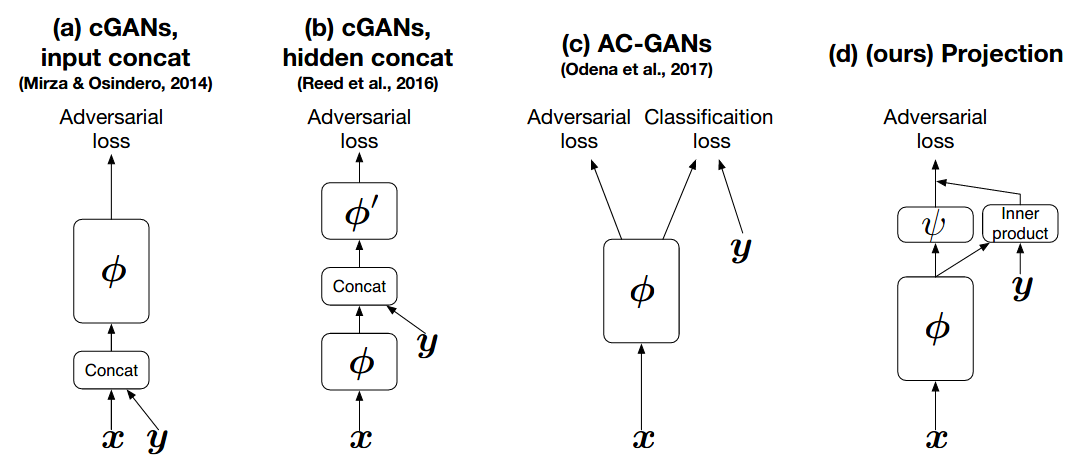
Figure from cGANs with Projection Discriminator paper

To study further, I’ll implement this and write a note about it later.

References

[1]: Generative Adversarial Networks

[2]: Conditional Generative Adversarial Nets

[3]: cGANs with Projection Discriminator